Di bidang kecerdasan buatan, neuro-fuzzy mengacu kombinasi dari jaringan saraf tiruan dan logika fuzzy. Neuro-fuzzy diusulkan oleh J. S. R. Jang. Hasil hibridisasi neuro-fuzzy dalam sistem cerdas hibrida yang mensinergikan kedua teknik dengan menggabungkan gaya penalaran manusia-seperti sistem fuzzy dengan belajar dan struktur koneksionis dari jaringan saraf. Neuro-fuzzy hibridisasi secara luas disebut sebagai Fuzzy Neural Network (FNN) atau Sistem Neuro-Fuzzy (NFS) dalam literatur. sistem neuro-fuzzy (istilah yang lebih populer digunakan selanjutnya) menggabungkan gaya penalaran manusia-seperti dari sistem fuzzy melalui penggunaan fuzzy set dan model linguistik yang terdiri dari satu set IF-THEN aturan fuzzy. Kekuatan utama dari sistem neuro-fuzzy adalah bahwa mereka approximators universal dengan kemampuan untuk meminta ditafsirkan IF-THEN aturan.

Kekuatan sistem neuro-fuzzy melibatkan dua persyaratan yang bertentangan dalam pemodelan kabur: interpretability vs akurasi. Dalam prakteknya, salah satu dari dua sifat berlaku. neuro-fuzzy dalam bidang penelitian pemodelan kabur dibagi menjadi dua wilayah: pemodelan kabur linguistik yang difokuskan pada interpretability, terutama model Mamdani; dan pemodelan kabur tepat yang difokuskan pada akurasi, terutama Takagi-Sugeno-Kang (TSK) model.
Meskipun umumnya dianggap realisasi dari sistem fuzzy melalui jaringan koneksionis, istilah ini juga digunakan untuk menggambarkan beberapa konfigurasi lainnya termasuk:
Ini harus menunjukkan bahwa interpretability dari Mamdani -jenis sistem neuro -fuzzy bisa hilang . Untuk meningkatkan interpretability sistem neuro -fuzzy , langkah-langkah tertentu harus diambil , dimana aspek penting dari interpretability sistem neuro -fuzzy juga dibahas . [ 1 ]
Sebuah garis penelitian baru-baru membahas kasus pertambangan aliran data , di mana sistem neuro - fuzzy berurutan diperbarui dengan sampel yang masuk baru pada permintaan dan on-the - fly . Dengan demikian , pembaruan sistem tidak hanya mencakup adaptasi rekursif dari parameter model , tetapi juga evolusi dinamis dan pemangkasan komponen Model ( neuron , aturan ) , untuk menangani konsep melayang dan dinamis mengubah perilaku sistem secara memadai dan untuk menjaga sistem / model " up - to-date " kapan saja . survei komprehensif dari berbagai sistem neuro -fuzzy berkembang pendekatan dapat ditemukan di [ 2 ] dan [3].
Pseudo outer-product-based fuzzy neural networks
Pseudo outer-product-based fuzzy neural networks( "POPFNN") adalah keluarga sistem neuro-fuzzy yang didasarkan pada model kabur linguistik. [4]
Tiga anggota POPFNN ada dalam literatur:
POPFNN-AARS (S), yang didasarkan pada perkiraan Analogical Penalaran Skema [5]
POPFNN-CRI (S), yang didasarkan pada umumnya diterima Aturan Komposisi fuzzy Inference [6]
POPFNN-TVR, yang didasarkan pada Kebenaran Nilai Pembatasan
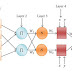
The "POPFNN" arsitektur jaringan saraf lima lapisan di mana lapisan dari 1 sampai 5 disebut: lapisan input linguistik, lapisan kondisi, lapisan aturan, lapisan konsekuen, keluaran lapisan linguistik. The fuzzification dari input dan defuzzifikasi dari output masing-masing dilakukan oleh masukan linguistik dan output lapisan linguistik sedangkan inferensi fuzzy secara kolektif dilakukan oleh aturan, kondisi dan konsekuensi lapisan.
Proses pembelajaran POPFNN terdiri dari tiga tahap:
Generasi keanggotaan Fuzzy
Identifikasi aturan Fuzzy
Diawasi fine-tuning
Berbagai algoritma generasi keanggotaan kabur dapat digunakan: Learning Vector Quantization (LVQ), Fuzzy Kohonen Partisi (FKP) atau Discrete Incremental Clustering (DIC). Umumnya, algoritma POP dan varian LazyPOP yang digunakan untuk mengidentifikasi aturan fuzzy.
Referensi

Kekuatan sistem neuro-fuzzy melibatkan dua persyaratan yang bertentangan dalam pemodelan kabur: interpretability vs akurasi. Dalam prakteknya, salah satu dari dua sifat berlaku. neuro-fuzzy dalam bidang penelitian pemodelan kabur dibagi menjadi dua wilayah: pemodelan kabur linguistik yang difokuskan pada interpretability, terutama model Mamdani; dan pemodelan kabur tepat yang difokuskan pada akurasi, terutama Takagi-Sugeno-Kang (TSK) model.
Meskipun umumnya dianggap realisasi dari sistem fuzzy melalui jaringan koneksionis, istilah ini juga digunakan untuk menggambarkan beberapa konfigurasi lainnya termasuk:
- Berasal aturan fuzzy dari jaringan RBF terlatih.
- Fuzzy tala berdasarkan logika parameter pelatihan jaringan saraf.
- kriteria fuzzy logic untuk meningkatkan ukuran jaringan.
- Menyadari fungsi keanggotaan kabur melalui algoritma pengelompokan dalam belajar tanpa pengawasan di SOMS dan jaringan saraf.
- Mewakili fuzzification, inferensi fuzzy dan defuzzifikasi melalui multi-lapisan makan-maju jaringan koneksionis.
Ini harus menunjukkan bahwa interpretability dari Mamdani -jenis sistem neuro -fuzzy bisa hilang . Untuk meningkatkan interpretability sistem neuro -fuzzy , langkah-langkah tertentu harus diambil , dimana aspek penting dari interpretability sistem neuro -fuzzy juga dibahas . [ 1 ]
Sebuah garis penelitian baru-baru membahas kasus pertambangan aliran data , di mana sistem neuro - fuzzy berurutan diperbarui dengan sampel yang masuk baru pada permintaan dan on-the - fly . Dengan demikian , pembaruan sistem tidak hanya mencakup adaptasi rekursif dari parameter model , tetapi juga evolusi dinamis dan pemangkasan komponen Model ( neuron , aturan ) , untuk menangani konsep melayang dan dinamis mengubah perilaku sistem secara memadai dan untuk menjaga sistem / model " up - to-date " kapan saja . survei komprehensif dari berbagai sistem neuro -fuzzy berkembang pendekatan dapat ditemukan di [ 2 ] dan [3].
Pseudo outer-product-based fuzzy neural networks
Pseudo outer-product-based fuzzy neural networks( "POPFNN") adalah keluarga sistem neuro-fuzzy yang didasarkan pada model kabur linguistik. [4]
Tiga anggota POPFNN ada dalam literatur:
POPFNN-AARS (S), yang didasarkan pada perkiraan Analogical Penalaran Skema [5]
POPFNN-CRI (S), yang didasarkan pada umumnya diterima Aturan Komposisi fuzzy Inference [6]
POPFNN-TVR, yang didasarkan pada Kebenaran Nilai Pembatasan
The "POPFNN" arsitektur jaringan saraf lima lapisan di mana lapisan dari 1 sampai 5 disebut: lapisan input linguistik, lapisan kondisi, lapisan aturan, lapisan konsekuen, keluaran lapisan linguistik. The fuzzification dari input dan defuzzifikasi dari output masing-masing dilakukan oleh masukan linguistik dan output lapisan linguistik sedangkan inferensi fuzzy secara kolektif dilakukan oleh aturan, kondisi dan konsekuensi lapisan.
Proses pembelajaran POPFNN terdiri dari tiga tahap:
Generasi keanggotaan Fuzzy
Identifikasi aturan Fuzzy
Diawasi fine-tuning
Berbagai algoritma generasi keanggotaan kabur dapat digunakan: Learning Vector Quantization (LVQ), Fuzzy Kohonen Partisi (FKP) atau Discrete Incremental Clustering (DIC). Umumnya, algoritma POP dan varian LazyPOP yang digunakan untuk mengidentifikasi aturan fuzzy.
Referensi
- Y. Jin (2000). Fuzzy modeling of high-dimensional systems: Complexity reduction and interpretability improvement. IEEE Transactions on Fuzzy Systems, 8(2), 212-221, 2000
- E. Lughofer (2011). Evolving Fuzzy Systems: Methodologies, Advanced Concepts and Applications. Springer Heidelberg
- N. Kasabov (2007). Evolving Connectionist Systems: The Knowledge Engineering Approach - Second Edition. Springer, London
- Zhou, R. W., & Quek, C. (1996). "POPFNN: A Pseudo Outer-product Based Fuzzy Neural Network". Neural Networks, 9(9), 1569-1581.
- Quek, C., & Zhou, R. W. (1999). "POPFNN-AAR(S): a pseudo outer-product based fuzzy neural network." IEEE Transactions on Systems, Man and Cybernetics, Part B, 29(6), 859-870.
- Ang, K. K., Quek, C., & Pasquier, M. (2003). "POPFNN-CRI(S): pseudo outer product based fuzzy neural network using the compositional rule of inference and singleton fuzzifier." IEEE Transactions on Systems, Man and Cybernetics, Part B, 33(6), 838-849.